
 |
Auditory Localization in the Near-Field |

|
|
IntroductionOver the past century many researchers have studied the process of auditory localization. The vast majority of this research, however, has concentrated only on sound sources that are relatively distant from the listener (1 m or more). This has been the most convenient region for studying localization, in part, because the head-related transfer function (HRTF) is essentially independent of distance beyond a meter. In contrast, as the sound source approaches the head, the primary localization cues change drastically. Interaural intensity differences (IIDs) increase dramatically as distance decreases, while interaural time delays (ITDs) remain constant. This systematic variation of the HRTF in the near-field region may allow listeners make absolute auditory distance judgments for nearby sources, and provide the means for significantly improving the capabilities of virtual audio displays. This paper examines some of the issues involved in near-field localization, and describes the results of a simple mathematical model that can predict localization performance at distances less than 1 m.
The Importance of the Near-FieldIn physical acoustics, the near-field is defined as the region of space within a fraction of a wavelength away from a sound source. According to this definition, the outer boundry of the near-field region varies inversely with frequency. In terms of human localization, we will designate the near-field as region of space within 1 m of the center of the listener's head, and the "far-field" as the region at distances greater than 1 m. The near-field is important to virtual audio displays in several respects. It is essentially the only region of space where binaural localization cues vary with source distance. This implies that it is also the only region where the listener will be able to make judgments about the distance of a sound source with no a priori information about the intensity or spectrum of the source. In addition, the near-field is the region of space within "arm's reach" of the listener and, therefore, the only region containing objects that the listener can physically interact with. As multimodal virtual environments combining auditory, haptic, and visual displays are developed, accurate auditory representations of nearby sources will become increasingly important. Finally, it is the region of space most naturally associated with urgent auditory information. A sound that appears to be very close to the head will receive a high-priority response from the listener. Despite these considerations, very little is known about localization in the near-field.
Near-Field Localization CuesAuditory localization in the near-field must rely on the same basic types of cues as far-field localization. The sound approaching each eardrum from the source is shaped by interactions with the head, torso, and pinna, resulting in the HRTF. Specifically, the HRTF is the ratio of the sound pressure at the eardrum to the sound pressure that would exist at the center of the head if the head were removed. In general, the sound arriving at the ear further from the source is attenuated and delayed relative to the sound arriving at the ear closer to the source. This generates an interaural intensity difference (IID) and an interaural time delay (ITD). Interaural information dominates auditory localization in the horizontal plane. The spectral shaping of the localization cues helps differentiate between source locations that are equally distant from both ears (the so-called "cones of confusion"), including sound sources in the median plane. Thorough summaries of auditory localization in general are given in (Blaurt, 1983) and (Middlebrooks et. al, 1991). As the source approaches the head, the ratio of distances from the source to the near and far ears increases, and the effects of head-shadowing are amplified, causing the interaural intensity difference to increase. The spectral shaping caused by the head and pinnae may also change as the source enters the physical acoustic near-field and the curvature of the sound field increases. The interaural delay, which results from the absolute difference in path length from the source to the ears, remains approximately constant as distance decreases. Possible distance cues for sources in a free-field are summarized in Coleman (1963). The next section discusses a mathematical model of auditory localization cues in the near-field.
Mathematical Model of Near-Field Localization CuesAlthough the actual shapes of the head, torso, and pinnae are complex and, therefore, difficult to model mathematically, a first order approximation of the head-related transfer function can be generated by modeling the head as a rigid sphere, 18 cm in diameter, with pressure sensitive ears at two diametrically opposite points on the sphere's surface. The transfer function from a sound source to a point on the surface of a sphere has been thoroughly examined in many texts on physical acoustics; however, most of these derivations have assumed a distant source. Manual calculations for the pressure on a rigid sphere due to a nearby sound source were first performed by Stewart in 1911 and by Hartley and Frey in 1921. More recently, Rabinowitz et. al. (1993) described a model (based on derivations by Morse and Ingard (1968) that can calculate the pressure generated on the surface of a sphere by a velocity point source at arbitrary distances from the sphere. This model was originally developed to examine the relationship between frequency scaled HRTFs and actual HRTFs for a magnified head, but it is equally applicable for modeling HRTFs for nearby point sources. According to this model, the pressure on the surface of a sphere due to a nearby point source is 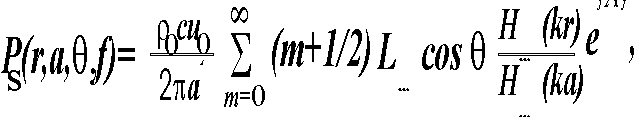 where r is the source distance (to the center of the sphere), a is the radius of the sphere (9 cm), q is the angle between the point on the surface of the sphere and the direct path to the source, f is the frequency, and k is the wave number 2pf/c . The constant u0 is the volume velocity of the point source, r0 is the density of air (1.18 kg/m3), and c is the velocity of sound (343 m/s). Lm(cos q) is the Legendre polynomial function in cos q, Hm(kr) is the spherical Hankel function in kr, and H’m(ka) is the derivative of the spherical Hankel function with respect to ka.
This equation can be used to determine the interaural intensity differences (IIDs) and interaural time delays (ITDs) for any direction and any distance relative to the head simply by taking the ratio of the pressure at the left ear to the pressure at the right ear. Figure 1 shows some polar plots of the IID where position is defined with q= 0o for a source directly in front of the listener. At 500 Hz the IID smoothly increases as the source moves to the side of the head. At higher frequencies, there are indications of the acoustic "bright spot" at the point on the surface of the sphere directly opposite the source. The sound waves diffracting around the sphere converge in phase at this point, resulting in an unusually large pressure. This causes high frequency IIDs to be relatively small—
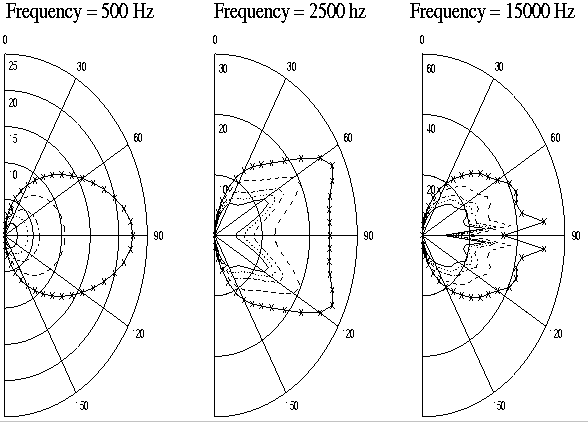  Figure 1: Interaural Intensity Differences (in dB) as a function of distance and direction
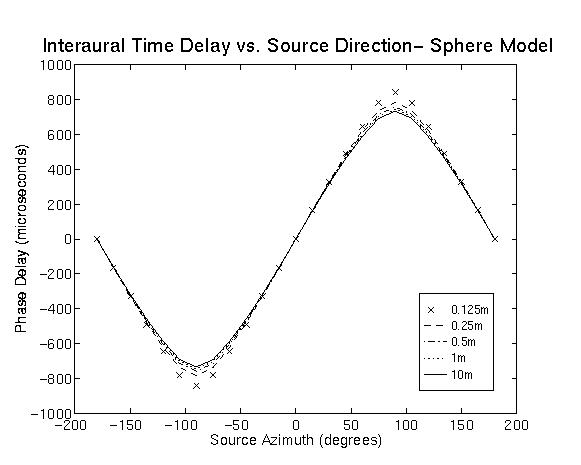 Figure 2: Mean phase delay vs. source direction and distance in the vicinity of q= 90o degrees. This is clearly seen in the "butterfly" shape of the polar plot at 2.5 kHz, and in the sharper notch in the IID at 90o at 15 kHz. This bright spot is an artifact of the perfect spherical shape assumed by the model, and will not be present in real HRTFs at higher frequencies where the irregular features of the head are significant in relation to the wavelength of the sound. The IIDs increase significantly as distance decreases below 1 m. For example, the maximum IID at 500 Hz increases from 2 dB to 4 dB as the source goes from 10 m to 1 m, but from from 4 dB to nearly 25 dB as the source moves from 1 m to 0.125 m. Similar results are seen at 2.5 kHz and 15 kHz. The IID at 500 Hz is more striking because there are essentially no low frequency interaural intensity differences at low frequencies when the source distance is greater than 1m. IIDs in this region occur only for near-field sources, and very little is known about the perceptual implications of these low frequency IIDs. Figure 2 shows the interaural time differences as a function of direction and distance. These were calculated by taking the average (unwrapped) interaural phase delay at 400 frequencies from 0 Hz to 6400 Hz. The results show that ITDs are roughly independent of distance except near |q|=90o. In this region, the time delay can be as much as 100 ms greater at 0.125 m than at 10 m, but listeners are relatively insensitive to changes in time delays above 700 ms (Toole et. al, 1965). Therefore, perceptually, the changes in time delay with distance are insignificant compared to the changes in the interaural intensity difference. The just noticeable difference (JND) in the interaural intensity difference at 500 Hz has been measured by Hershkowitz and Durlach (1969), and is approximately 0.8 dB across a wide range of IIDs. This information can be used with the results from the sphere model of the head to estimate the smallest detectable decrease in distance DD for a 500Hz source as a function of source distance D and direction q. The left panel of Figure 3 shows the IID predicted by the sphere model as a function of distance for a 500 Hz source at locations 30o, 60o, and 90o to the side of the listener; the right panel shows the percentage decrease in distance DD/D necessary to generate a 0.8 dB increase in IID. A subject would be expected to detect these percentage decreases in distance if he or she was asked to judge changes in the distance of a sound source with a random overall amplitude on each presentation. These calculations show that performance decreases (DD/D increases) as the source approaches the median plane and the distance to the source increases. For a source at q = 90o, DD/D ranges from 12% at 0.1 m to 40% at 1 m. Of course, if the overall intensity is not randomized across presentations it will dominate as a relative distance cue. Humans are sensitive to changes in intensity of approximately 1 dB (Miller, 1947), which would correspond to a constant 12.2% change in distance. Finally, note that a model of near-field localization based on interaural differences for a perfectly spherical head predicts that humans will be unable to identify the distance of a sound source in the median plane without a priori information about the signal. However, it is possible that subtler cues, including changes in the spectral content of the signal reaching the ears due to interactions between the head and the sound field in the acoustic near-field, will allow rough estimates of distance even in the median plane.
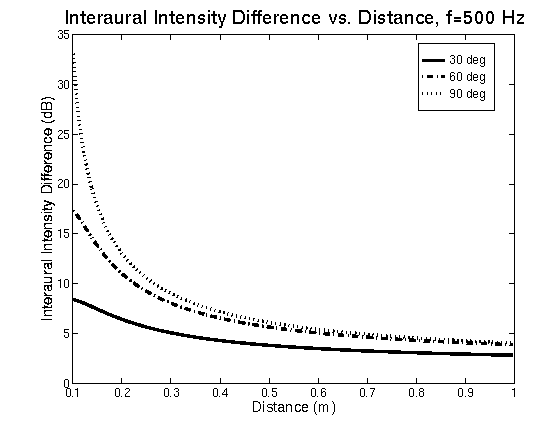 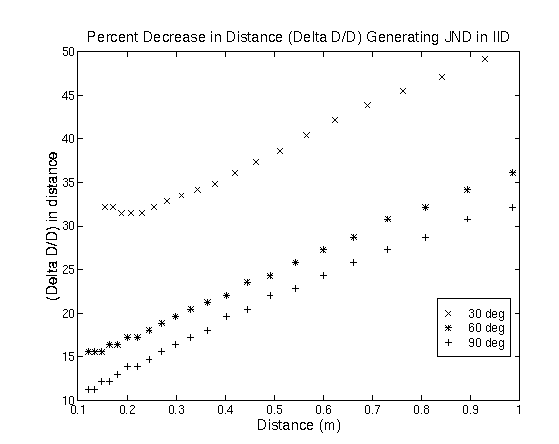 Figure 3: Model for distance discrimination of a 500 Hz signal in the near-field
ConclusionTo make accurate localization judgments in the near-field region, the auditory system must account for changes in the localization cues due to variations in distance. Almost no information is available to evaluate how well humans can localize in the near field, and we know of no published data measuring the head-related transfer function in the near-field with either human subjects or an anthropomorphic mannequin. Current research efforts are addressing both of these deficiencies. A better understanding of human localization performance in the near-field should enable the development of effective virtual audio displays for near-field sources.
ReferencesBlauert J. (1983). Spatial Hearing. MIT Press, Cambridge, MA. Morse, P.M. and Ingard, K.U. (1968). Theoretical Acoustics. McGraw-Hill.
Author InformationDouglas S. Brungart and William R. Rabinowitz Research Laboratory of Electronics, MIT 77 Massachusetts Ave. Cambridge, MA 02139
|
